Chapter 14. Calorimetry and Hess’s Law

Objectives

Laboratory 6
false
false
  • Calibrate and use a calorimeter to determine enthalpy changes for two different reactions. Relate temperature measurements and heat transferred by using heat capacities or specific heat.
  • Use thermochemical equations to relate the change in enthalpy to the amount of substance involved in the reaction.
  • Use Hess’s law to determine enthalpy changes for chemical reactions.

Discussion

Most chemical and physical processes are accompanied by a change in energy. The system can either gain or lose energy. The energy can be in the form of heat, light, or electrical energy. In this lab we will study reactions in which energy is evolved as heat. Enthalpy, H, is a thermodynamic function that involves the flow of heat occurring at a constant pressure. Enthalpy is equal to the internal energy of the system, E, plus the product of the volume and pressure:

H = E + PV

Energy, pressure, and volume are all state functions. A state function is a property of the system that is determined by the state of that system, and not by how it got there. Since energy, pressure, and volume are state functions, enthalpy is also a state function. When a change occurs at constant pressure, the change in enthalpy, ΔH, is equal to the heat lost or gained:

ΔH = q

The First Law of Thermodynamics states that energy is conserved. From this we may state that the heat lost by the system is equal to the heat gained by the surroundings, or vice versa. Thus, the sign of q is indicative of the direction of heat flow.

When a system gains heat from the surroundings, q is positive, so ΔH is positive and this is referred to as an endothermic process. Likewise, when a system loses heat q is negative, ΔH is negative, and this is an exothermic process.

A change in enthalpy for a chemical reaction is called the enthalpy of reaction or heat of reaction, ΔHrxn, and the energy units commonly used are kilojoules, kJ.

Since ΔH = ΔHfinal – ΔHinitial, the

ΔHrxn = ΔHproducts − ΔHreactants

The following are some guidelines helpful to remember when using ΔH:

  1. Thermochemical equations are written for molar quantities.

    H2(g) + ½O2(g) → H2O(l)      ΔH = –286 kJ
    The value −286 kJ is the ΔH for one mole of H2O(l) formed, and fractional coefficients for these reactants are acceptable. The ΔH for 2 moles of H2O(l) formed would be 2 × (−286 kJ) = −572 kJ, or twice as much.
  1. The physical state of each substance is important as the enthalpy depends on their states. If we look at the thermochemical equation for the formation of H2O(g)

    H2(g) + ½O2(g) → H2O(g)      ΔH = 2242 kJ
    we notice the ΔH is not the same. Therefore it is important to indicate the states for all reactants and products.
  1. The sign of ΔH is important. In our example the sign of ΔH is negative, indicating that the enthalpy of the products is less than the enthalpy of the reactants and energy is given off in the process. This is an exothermic process. If the reaction were reversed

    H2O(l) → H2(g) + ½O2(g)      ΔH = 286 kJ
    the reactants are now the products and vice versa, thus the sign of ΔH changes and this process is endothermic.

Hess’s Law

Many ΔH of reactions have been measured and tabulated and are available to look up. It is possible to calculate the ΔH of a reaction by using the collected ΔH values from other reactions. Hess’s law of heat summation states that if a reaction is completed in a series of steps the ΔH for the entire reaction is the sum of the ΔH values for the individual steps. This provides a way to calculate energy changes for reactions that may be difficult to measure. Consider the following example:

CuS(s) + O2(g) → CuS(s) + SO2(g)      ΔH = ?

We may use Hess’s law to determine ΔH for this reaction: in the tables we can find the equations and their ΔH values for the steps that make up this reaction:

CuS(s) → Cu(s) + S(s)      ΔH = 48.5 kJ
S(s) + O2(g) → SO2(g)      ΔH = –296.9 kJ

Now to find ΔH for our reaction we can simply add the equations and add the ΔH values:

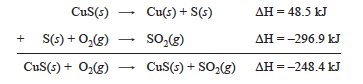
And we have calculated the ΔH for the overall reaction. This example is straightforward. However, sometimes the amount of reactants and products need to be adjusted to reach the overall reaction. In these cases we need to use the following rules:

  1. If an equation is multiplied by a factor, ΔH is multiplied by that factor.
  2. If an equation is reversed, the sign of ΔH is changed.
  3. All substances not in the overall reaction must cancel out.

Consider the following example. We want to know the change in enthalpy for the following reaction.

Fe2O2(s) + 3 CO(g) → 2 Fe(s) + 3 CO2(g)      ΔH = ?

We know ΔH values for the two equations below.

4 Fe(s) + 3 O2(g) → 2 Fe2O3(s)      ΔH = −1644.4 kJ
CO(g) + ½O2(g) → CO2(g)      ΔH = −283.0 kJ

To make these two equations add up to the desired equation, the first equation must be divided by 2 and reversed, and the second equation must be multiplied by 3. Note how the corresponding ΔH values change.

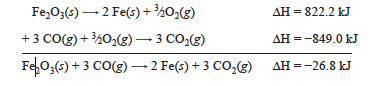
Question 6.1: Calculate the enthalpy change for the reaction

P4O6(s) + 2 O2(g) → P4O10(g)

Given the following enthalpies of reaction:

P4(s) + 3 O2(g) → P4O6(g) ΔH = –1640.1 kJ

P4(s) + 5 O2(g) → P4O10(g) ΔH = –2940.1 kJ

Calorimetry

Calorimetry is an experimental way to measure the heat flow. A calorimeter is an insulated vessel in which the heat absorbed or evolved can be determined by measuring the change in temperature. As introduced in lab 1, the temperature is a measure of the average kinetic energy of the particles in a substance. The heat capacity, C, is the amount of heat required to increase an object’s temperature by 1 K (or 1 °C). The molar heat capacity, Cm, is the heat capacity per one mole and the specific heat, Cs, is the heat capacity of one gram of substance. The specific heat is determined experimentally by measuring the change in temperature, ΔT, a substance with mass m undergoes while gaining or losing heat, q:

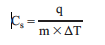
Data Analysis and This Lab

This lab has four parts. In Part A you will first need to calibrate your calorimeter. Calibration of the calorimeter is required so that an observed temperature change corresponds to a known heat change. The process is based on the First Law of Thermodynamics:

heat lost by the system = heat gained by the surroundings

The system in the first part of the experiment consists of two copper cylinders which are heated to near 100 °C. The surroundings consist of a foam cup (the calorimeter) containing a measured amount of water at room temperature. The heat that is lost by the copper is equal to the heat gained by the water plus the heat gained by the calorimeter:

−qCu = qwater + qcalorimeter

The heat lost or gained may be determined by using the known specific heat, Cs, the measured mass, m, and the change in temperature, ΔT:

q = Cs × m × ΔT

Near room temperature, the specific heat of copper is 0.385 J/(g × °C) and the specific heat of water is 4.18 J/(g × °C). The mass of copper and of water is measured from the balance. The change in temperature for the copper cylinders is the final temperature, Tf, minus the temperature measured at boiling, Tb. The change in temperature of the water is the final temperature, Tf, minus the initial temperature, Ti, both values taken from the graph (for details, see graph analysis).

qCu = 0.385 J/(g × °C) × mass of Cu in g × (Tf – Tb) °C
qwater = 4.18 J/(g × °C) × mass of water in g × (Tf – Ti) °C

Knowing the qCu and qwater, we now know the qcalorimeter.

qcalorimeter = −(qCu + qwater)

We can use this to solve for the specific heat of our calorimeter, C, by using ΔT:

qcalorimeter = C × (Tf – Ti) °C

The heat capacity of the calorimeter will probably be a rather small number but it should be positive. If a negative value is calculated use zero for C instead of the calculated number.

Question 6.2: Two solid objects, A and B, are placed in boiling water and allowed to come to temperature there. Each is then lifted out and placed in separate beakers containing 1000 g of water at 10.0 °C. Object A increases the water temperature by 3.50 °C; B increases the water temperature by 2.60 °C.

Which object has the larger heat capacity?

In Part B of the experiment, ΔH for the acid–base neutralization reaction is calculated.

The heat produced in the neutralization reaction is absorbed by the HCl solution, the NaOH solution, and the calorimeter:

−qrx1 = qHCl + qNaOH + qcalorimeter

We will assume the specific heats of NaOH and HCl solutions are the same as water, 4.18 J/ (g × °C). The mass of the HCl solution is collected in step 9. The mass of the NaOH solution is calculated from the volume used in step 12 and the density 1.083 g/mL. Tf and Ti for solutions are both taken from the graph (for details, see graph analysis) and To is the original measured temperature of the NaOH solutions, step 10:

qHCl = 4.18 J/(g × °C) × mass of HCl solution in g × (Tf – Ti) °C
qNaOH = 4.18 J/(g × °C) × mass of NaOH solution in g × (Tf – To) °C
qcalorimeter = C × (Tf – Ti) °C

The sum of qHCl, qNaOH, and qcalorimeter is equal to the heat produced in the neutralization reaction for the number of moles reacted. We need to know the number of moles reacted and calculate that by using the volume and molarity of the limiting reactant. Lastly we divide the heat of the reaction by the number of moles to obtain the enthalpy change for the reaction, ΔH1:

ΔH1 = (qrx1/moles)

Question 6.3: Why is it reasonable to assume the specific heats of NaOH and HCl solutions are the same as water, 4.18 J/(g × °C)?

  1. Most of the particles in NaOH and HCl solutions are water molecules and the product of the reaction is water.
  2. The specific heats of all liquids are very close to 4.18 J/(g × °C).
  3. Na+ and Cl– will combine to form the salt NaCl, and this removes the particles from the solution leaving pure water.
  4. The specific heat value is not very important because it appears in different equations and will cancel out.

In Part C of the lab the ΔH for the reaction of magnesium with acid is determined.

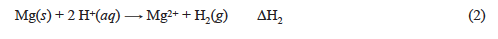
Similar to the previous sections, the heat produced by the reaction of magnesium and hydrochloric acid is absorbed by the solution and calorimeter:

−qrx2 = qsoln + qcalorimeter

The specific heat of the more concentrated HCl solution here is 3.72 J/(g × °C). The mass of the solution is obtained in step 16. The initial and final temperatures are obtained from the graph (for details, see graph analysis).

qsoln = 3.72 J/(g × °C) × mass of solution in g × (Tf – Ti) °C
qcalorimeter = C × (Tf – Ti) °C

The sum of these two terms is qrxn2, the heat of our reaction. Using the mass of magnesium collected in step 15 we may find the enthalpy, ΔH2, by diving qrxn2 by the number of moles of Mg.

Lastly, in Part D, Hess’s law will be used to calculate the ΔH for two more reactions:

For determination of ΔH3 you will use the proper combination (multiplying and reversing as needed) of equations 1 and 2. To determine ΔH4 you will need to use the proper combinations of equation 3 with 5 and 6 (listed below).

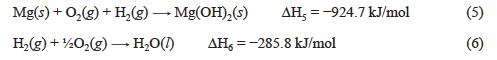
Question 6.4: When a 3.76 g sample of solid ammonium nitrate dissolves in 60.0 g of water in a coffee-cup calorimeter the temperature drops from 22.0 °C to 16.9 °C. Calculate ΔH (in kJ/mol NH4NO3) for the solution process:

NH4NO3(s) → NH4+(aq) + NO3–(aq)

Assume that the specific heat of the solution is the same as that of pure water, and determine whether this process is endothermic or exothermic.

Graphing Your Data

For Parts A, B, and C, graphs must be constructed to determine the initial and final temperatures of the system. The graphs of temperature versus time will be similar to the figure below.

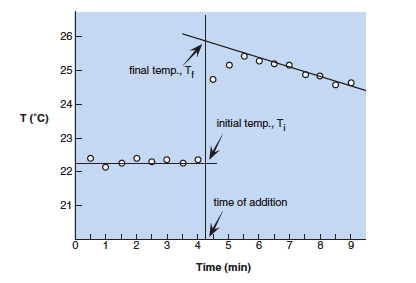
Temperature readings are taken at the beginning to establish the initial temperature, Ti; readings should be fairly constant. If the addition of copper, NaOH, or magnesium is made after 4.0 minutes, the time of addition is estimated between 4.0 and 4.5 minutes. A vertical line is drawn at this time. The addition causes a sharp increase in temperature followed by a slow decrease as heat is lost to the surroundings. A constant rate of decrease establishes a line that can be extrapolated back to the vertical line at time of addition. The temperature at which the lines intersect is the final temperature, Tf. Notice that the final temperature is not the last temperature read nor is it the highest temperature read. It can only be obtained from the graph by extrapolation.

The best orientation is to put temperature on the y-axis and time on the x-axis. The time of addition line, Ti, and Tf, must be labeled along with the axes (and units). When using your graphing program (Excel works well) have a gridline drawn at every 0.1 °C and 0.1 min. Plot the points using a scatter graph with points only, axes labels and titles, and graph title. Print the graph and draw in lines for time of addition, Ti, and Tf by hand.

Materials Required

Equipment

  • 25-mL test tube
  • 100-mL graduated cylinder
  • digital thermometer
  • Styrofoam cup with lid
  • 400-mL beaker
  • 100-mL beaker
  • 10-mL pipet
  • water bath (600-mL beaker)
  • Bunsen burner, wire gauze
  • thin-walled rubber tubing
  • ring stand, ring

Chemicals

  • 2 copper cylinders
  • 3.0 M sodium hydroxide, NaOH
  • 3.0 M hydrochloric acid, HCl
  • 6 M hydrochloric acid, HCl
  • magnesium turnings

Common Equipment

  • top-loading balance

Cautions

Be careful to avoid burns from the ring, beaker, and the open flame.

Procedure

A. Calibration of the calorimeter.

Create three columns on a blank page in your notebook to collect the temperature data for Parts A, B, and C. Mark at the top A, B, C and record all temperatures to be used for the three graphs. Mark the time of addition.
  1. Obtain two copper cylinders and a Styrofoam cup with lid from your lab instructor. Check out a digital thermometer display and probe from the storeroom window (Student ID required).
  2. Set up a hot water bath using a 600-mL beaker, ring stand, and Bunsen burner. Weigh the two copper cylinders to the nearest 0.01 g. Carefully place the two copper cylinders in a 25-mL test tube. Place the test tube in the hot water bath and let the bath come to a boil while proceeding to the next step.
  3. Weigh the clean, dry Styrofoam cup to the nearest 0.01 g. Add 60 mL of distilled water to the cup and reweigh the cup and water to the nearest 0.01 g. Place the cup in a 400-mL beaker for stability
  4. After the test tube containing the copper cylinders has been boiling in water for at least 10 minutes, record the temperature of the boiling water bath, Tb, using the digital thermometer. After recording the temperature, run tap water over the probe to cool it back to room temperature.
  5. Record the temperature of the water in the cup every thirty seconds for four minutes. Keep the lid on the cup and keep the cup away from the hot water bath.
  6. Carefully remove the test tube containing the copper cylinders from the boiling water. Quickly dry off the test tube and dump the copper cylinders into the Styrofoam cup. Replace the lid immediately and record the temperature with the digital thermometer.
  7. Continue to record the temperature every thirty seconds for at least five minutes. Whenever readings are being taken, occasionally swirl the water in the cup to assure uniform temperature. Stop taking readings when a constant decrease in temperature is noted for four consecutive readings.
  8. Dump out the water and return the copper cylinders to your lab instructor now.
B. Measurement of ΔH for the neutralization reaction.
  1. Add 50 mL of distilled water to the cup, and pipet 10 mL of the standardized 3.0 M HCl solution into the water in the cup. Record the exact molarity of the HCl solution given on the bottle. Weigh the cup and HCl/H2O solution to the nearest 0.01 g.
  2. Obtain about 20 mL of 3.0 M NaOH solution. Record the exact molarity of the NaOH solution given on the bottle. Record the temperature, To, of the solution using the digital thermometer and use a small amount to rinse the pipet.
  3. Rinse the probe with distilled water, dry it, and use the digital thermometer to record the temperature of the solution in the cup every thirty seconds for four minutes. Occasionally swirl the cup. Keep the lid on the cup.
  4. Pipet 10 mL of the standardize NaOH solution into the HCl solution in the cup. Swirl the cup to mix the contents. Replace the lid and immediately record the temperature with the digital thermometer
  5. Continue to record the temperature every thirty seconds for at least five minutes. Stop taking readings when a constant decrease in temperature is noted for four consecutive readings.
  6. Dump out the solution and rinse the cup with distilled water.
C. Measurement of ΔHf for the Mg2+(aq).
  1. Weigh out 0.12 g of magnesium turnings to 0.0001 g on the analytical balance.
  2. Add 40 mL of distilled water and 20 mL of 6 M HCl to the cup. Weigh the cup and HCl solution to the nearest 0.01 g. Swirl the cup to mix the contents.
  3. Using the digital thermometer, record the temperature of the solution in the cup every thirty seconds for four minutes. Occasionally swirl the cup. Keep the lid on the cup.
  4. Carefully add the magnesium turnings to the HCl solution in the cup. Swirl the cup to mix the contents. Replace the lid and immediately record the temperature with the digital thermometer.
  5. Continue to record the temperature every thirty seconds for at least five minutes. Stop taking readings when a constant decrease in temperature is noted for four consecutive readings.
  6. Dump out the solution and rinse the cup with distilled water. Return the cup and lid to your instructor, and the digital thermometer to the storeroom window.
D. Determination of ΔH for two other reactions using Hess’s law.
  1. ΔH for the other reactions may be calculated by combining various equations and summing the corresponding enthalpies according to Hess’s Law.

Waste Disposal

All solutions may be rinsed down the drain.